Exercise 2: Monte-Carlo

The Law of Large Numbers and Monte-Carlo Estimation.

1. Write a function which generates a sample of \(10\) observations \(iid\) from a Gaussian distribution (with mean \(m=2\) and standard deviation \(s=3\), i.e. a variance of \(9\)) and that returns the variance estimate over this sample (using the var() function).

   var_est <- function(n = 10) {
       s <- rnorm(n, mean = 2, sd = 3)
       return(var(s))
   }

2. Use the the Monte-Carlo method to estimate the variance of the distribution generating this sample, by using multiple realizations (e.g. 5) of the standard-deviation estimate implemented above. Do it again with 1,000 realizations, thus illustrating the law of large number convergence.

   # Monte-Carlo method
   nMC <- 5  # Monte Carlo sample size
   varMC <- numeric(nMC)
   for (i in 1:nMC) {
       varMC[i] <- var_est(n = 10)
   }
   mean(varMC)  # LLN estimate 

   ## [1] 6.653662

   nMC <- 1000  # Monte Carlo sample size
   for (i in 1:nMC) {
       varMC[i] <- var_est(n = 10)
   }
   mean(varMC)  # LLN estimate

   ## [1] 9.126242

   When the sample size increases, the estimator becomes more precise. This illustrates the Law of Large Numbers.

   
   

Let’s now program a Monte-Carlo estimate of \(\pi\approx 3,1416\)

1. Program a function roulette_coord which has only one argument ngrid (representing the number of different outcomes possible on the roulette used) whose default is 35, generating the two coordinates of a point (between \(0\) and \(35\)) as a vector. Use the R function sample (whhose help page is accessible through the command ?sample). The function will return the vector of the 2 coordinates x and y generated this way.

   roulette_coord <- function(ngrid = 35) {
       x <- sample(x = 0:ngrid, size = 1)
       y <- sample(x = 0:ngrid, size = 1)
       return(c(x, y))
   }

2. Thanks to the formula to compute the distance bewteen 2 points: \(d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\), program a function computing the distance to the origin (here has coordinates \((\frac{ngrid}{2}, \frac{ngrid}{2})\)) that checks if the computed distance is less than the unit disk radius (\(R = \frac{ngrid}{2}\)). This function, called for instance inside_disk_fun(), will have 2 arguments: the vector p containing the coordinates of the points on the one hand, and the integer ngrid on the other hand. It will return a boolean value (TRUEor FALSE) indicating the point is inside the disk.

   inside_disk_fun <- function(p, ngrid = 35) {
       d <- sqrt((p[1] - ngrid/2)^2 + (p[2] - ngrid/2)^2)
       return(d <= ngrid/2)
   }

3. The surface ratio between the disk (radius \(\frac{ngrid}{2}\)) and the square (side length \(ngrid\)) is equal to \(\frac{\pi}{4}\). This means that the probability of sampling a point inside the disk rather than outside is \(\frac{\pi}{4}\). Using this result, a Monte Carlo estimate of \(\pi\) can be implemented by computing the average number of time sampled points fall inside the disk multiplied by 4. Program such a function with their only input being a boolean vector of size \(n\) (the number of sampled points), which is TRUE if the point is indeed inside the disk and FALSE otherwise.

   piMC <- function(in_disk) {
       return(4 * mean(in_disk))
   }

4. Using the code below, generate 200 points and plot the data generated. What is the corresponding Monte Carlo estimate of \(\pi\) ? Change npoints and comment. How could the estimation be improved (ProTip: try ngrid <- 1000 and npoints <- 5000) ?

   # Grid size (resolution)
   ngrid <- 35
   
   # Monte Carlo sample size
   npoints <- 200
   
   # Points generation
   pp <- matrix(NA, ncol = 2, nrow = npoints)
   for (i in 1:nrow(pp)) {
       pp[i, ] <- roulette_coord(ngrid)
   }
   
   # Estimate pi
   in_disk <- apply(X = pp, MARGIN = 1, FUN = inside_disk_fun, ngrid = ngrid)
   piMC(in_disk)
   
   # Plot first we initialise an empty plot with the right size using argument
   plot(x = pp[, 1], y = pp[, 2], xlim = c(0, ngrid), ylim = c(0, ngrid), axes = 0,
       xlab = "x", ylab = "y", type = "n")
   ## we tick the x and then y axes from 1 to ngrid
   axis(1, at = c(0:ngrid))
   axis(2, at = c(0:ngrid))
   ## we add a square around the plot
   box()
   ## we plot the grid (using dotted lines thanks to the argument `lty = 3`) onto
   ## which the points are sample
   for (i in 0:ngrid) {
       abline(h = i, lty = 3)
       abline(v = i, lty = 3)
   }
   ## we add the sampled points
   lines(x = pp[, 1], y = pp[, 2], xlim = c(0, ngrid), ylim = c(0, ngrid), xlab = "x",
       ylab = "y", type = "p", pch = 16)
   ## we add the circle display
   x.circle <- seq(0, ngrid, by = 0.1)
   y.circle <- sqrt((ngrid/2)^2 - (x.circle - ngrid/2)^2)
   lines(x.circle, y = y.circle + ngrid/2, col = "red")
   lines(x.circle, y = -y.circle + ngrid/2, col = "red")
   ## finally we color in red the points sampled inside the disk
   lines(x = pp[in_disk, 1], y = pp[in_disk, 2], xlim = c(0, ngrid), ylim = c(0, ngrid),
       xlab = "x", ylab = "y", type = "p", pch = 16, col = "red", cex = 0.7)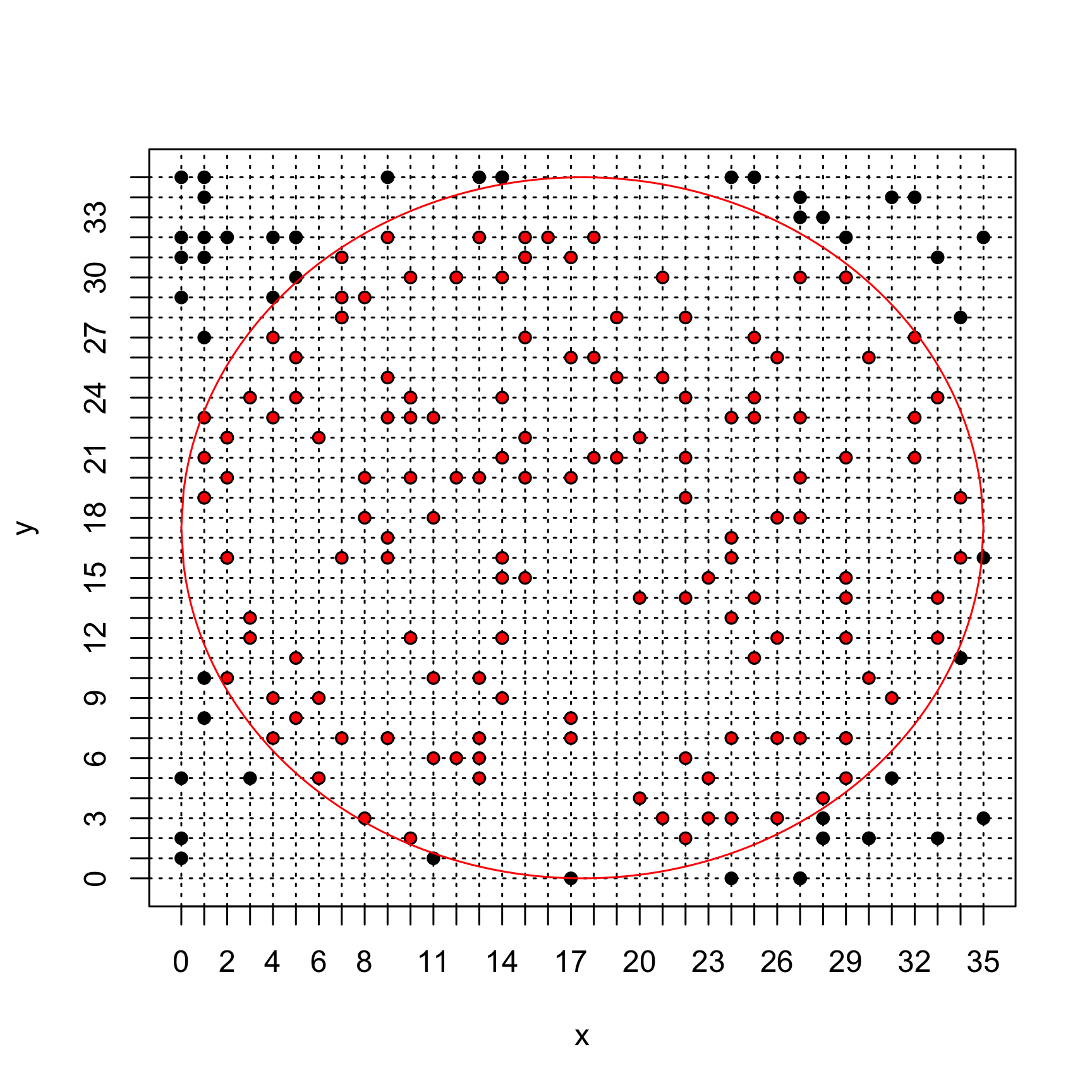

   

   When the sample size increase, the Monte Carlo estimator becomes more precise (LLN). However, if the grid is too coarse, \(\widehat{\pi}\) is underestimated (underestimating the disk surface by missing the bits near the edge). Therefore, increasing the number of points on the grid also improves the precision of the Monte Carlo estimation.